Prim-E-Proof

Ziel des Projektes:

Das Projekt „Prim-E-Proof“ (Primary Education and an Electronic Proof System) verfolgt das Ziel, substanzielle Lernumgebungen mit digitalen Medien (OpenSource Applets auf Tablet PCs) zur Unterstützung von Argumentations- und Beweisfähigkeiten in der Primarstufe zu generieren. Der Fokus des Projektes liegt darauf, Lehr- und Lernprozesse mit digitalen Lernumgebungen zu unterstützen.

Es soll ein Konzept zur Entwicklung von substanziellen Lernumgebungen zum präformalen Beweisen (Blum & Kirsch, 1991) abgeleitet werden (Designtheorie; siehe Forschungsdesign). Dabei werden mathematische (arithmetische) Sätze fokussiert, die in der Primarstufe präformal bewiesen werden können (z.B. mit Hilfe von Plättchenmustern). Dabei kann beispielsweise Bezug auf die Lehre vom Geraden und Ungeraden (Buch IX der Elemente des Euklid) genommen werden und es könnten Assoziativ-, Kommutativ- und Distributivgesetz in den Blick genommen werden. Im Sinne des Spiralprinzips könnte auch statt einer Plättchendarstellung über eine Darstellung der Produkte zweier Zahlen durch Flächeninhalte von Rechtecken nachgedacht werden, um über eine Anwendung des Applets zum präformalen Beweisen bspw. des Distributivgesetzes für natürliche Zahlen den Zahlenraum auf reelle Zahlen erweitern zu können und so das Applet auch für die Themengebiete binomische Formeln und quadratische Gleichungen anwenden zu können.

Zur Unterstützung von Lehrpersonen sollen folgende Funktionen im Applet umgesetzt werden: Der handelnde Umgang mit dem Tablet PC kann durch das computergestützte Tracking der Multi-Touch-Gesten der Kinder detektierbar gemacht und semiotisch ausgewertet werden. Huth (2013) stellt fest, dass insbesondere Gesten mindestens zeitweise die Funktion von eventuell aktuell nicht verfügbaren oder nicht möglichen Inskriptionen übernehmen können. In einem Kooperationsprojekt mit der Goethe-Universität Frankfurt am Main wird dies untersucht. Die Ergebnisse dieser Untersuchung fließen in die automatisierte Erfassung des handelnden Umgangs mit Lehr-Lernmaterialien, um u.a. maßgeschneiderte Interaktivität für Schüler*innen sowie eine sofortige Diagnosefunktion für die Lehrkraft anzubieten.

Projektbeschreibung:

Ausgehend von der Hochschullehre sollte im Rahmen des Projektes „E-Proofs“ ein E-Proof-System als Beweispuzzle mit ungeordneten Beweisfragmenten, das durch falsche Beweisfragmente ergänzt wird, umgesetzt werden (Platz et al., 2018). Im Rahmen einer Beobachtungsstudie stellte sich heraus, dass viele Studierende bei der Entwicklung einer Beweisidee scheiterten (vgl. auch (Grieser, 2015; Götze, 2019). Bei der Förderung der Entwicklung von Beweisideen sollte bereits in der Primarstufe angesetzt werden, da sich das Beweisen sonst für Lernende, wenn sie an weiterführenden Schulen oder an der Universität auf dieses stoßen, eher fremdartig und nicht wie eine natürliche Erweiterung ihrer früheren mathematischen Erfahrungen anfühlt, (Stylianides, 2016). Dies lässt sich durch die Grundannahme „[…], dass ein Lernen ohne Brüche nur möglich ist, wenn der Mathematikunterricht vom Kindergarten bis zum Abitur als zusammenhängendes Ganzes gesehen wird und wenn er stufenübergreifend auf einem authentischen Bild von der Mathematik als ‚Wissenschaft der Muster‘ fußt“, (Wittmann, 2014, S.213) stützen. Davon ausgehend entstand das Projekt „Prim-E-Proof“.

Auf Basis einer empirischen Pilotstudie, die mit 23 Viertklässer*innen einer nordrhein-westfälischen Grundschule durchgeführt wurde, wurde die Lernenden- bzw. Nutzerperspektive beim Bearbeiten der ersten Version einer Lernumgebung rekonstruiert (Platz, im Druck a; Platz, angenommen; Platz & Schlicht, im Druck), um Rückschlüsse für die Weiterentwicklung dieser ziehen zu können. Im Zentrum stand die Aufgabenstellung „Wenn man zwei ungerade Zahlen miteinander addiert, erhält man immer eine gerade Zahl. Stimmt das? Begründe!“, (u. a. Platz, 2019a). Zur Bearbeitung verwendeten die Schüler*innen das Wendeplättchen-Applet (Platz, 2019b) auf einem Tablet PC pro Zweiergruppe. Es sollte die Entwicklung einer Beweisidee durch die Annäherung an einen präformalen Beweis (Blum & Kirsch, 1991) angeregt werden. Scheinbar konnte noch kein Beweisbedürfnis (Kothe, 1979) bei den Schüler*innen geweckt werden, (u.a. Platz, im Druck), da die Schüler*innen zwar Muster erzeugen konnten, diese aber nicht erklären oder beschreiben konnten. Eine Betrachtung eines Musters als Ganzes kann nur in die Handlungen einer Zweiergruppe hineingedeutet werden. In einem Fall fand sogar eine Verweigerung der Aufgabe statt, da Plättchen als „kindisch“ empfunden wurden.

In einer weiterentwickelten Lernumgebung wird versucht ein Beweisbedürfnis durch die Erzeugung von Relevanzerlebnissen (Kothe, 1979) anzuregen, um eine Verbindung der Selbsttätigkeit der Schüler*innen mit dem mathematischen Denken herzustellen. Um ein solches für die Schüler*innen zu erzeugen, soll ein historischer Exkurs (Krauthausen, 2018) realisiert werden, um so die Lernumgebung in einen authentischen Kontext einzubetten. So kann ein Bezug zu den Herangehensweisen und Arbeitsmitteln der Pythagoreer, die Rechensteine zur Begründung arithmetischer Zusammenhänge verwendeten, hergestellt werden.

In einer neuen Version des Applets wurden Strukturierungshilfen (Walter, 2017) durch eine Gitterstruktur im Hintergrund sowie die Möglichkeit neben 1er-Plättchen auch 2er-, 5er- oder 10er-Stangen zu verwenden, um dem Zählen entgegenzuwirken, implementiert. Plättchen können gruppiert werden, Gruppierungen können gedreht und verschoben werden und gruppierte Plättchen können wieder in Einer zerlegt werden. Die Funktion des automatisierten Bildens von Rechtecken aus den Plättchen (mit ‚Nase‘ bei ungeraden Zahlen) ermöglicht eine stärkere Passung zwischen Handlung und mentaler Operation (Walter, 2017). Diese neue Lernumgebung wurde mit einem Schüler einer Tiroler Volksschule getestet. Es wurde deutlich, dass das Vorwissen der Schüler*innen großen Einfluss auf die Beweistätigkeiten dieser hat. Dieses soll in gezielten Vorübungen zum Beweisen (Fischer, 2004) aufgegriffen und weiterentwickelt werden. Dadurch soll auch die Vernetzung der Darstellungsebenen unterstützt werden, d. h. das Verständnis dafür, dass die Figurierung für alle ungeraden natürlichen Zahlen möglich ist: die ikonische Darstellung muss für den Lerner symbolisch werden (Lambert, 2012).

Forschungsdesign:

Um digitale Medien zugeschnitten auf Lernumgebungen gemeinsam mit diesen (weiter-)entwickeln zu können, wird eine Kombination aus Educational Design Research (u.a. Plomp, 2013; Hußmann et al., 2013; Prediger et al., 2012) und Design Science Research in Information Systems (Drechsler & Hevner, 2016) betrieben. Das Anliegen von Design Science Research ist es, Problemlösungen zu entwickeln und gründliche Bewertungen durchzuführen, um das Wissen über Design Sciences als Designtheorien zu kodifizieren. Design Science Research umfasst in der Regel die Erstellung eines Artefakts und/ oder einer Designtheorie, um den aktuellen Stand der Praxis sowie das vorhandene Forschungswissen zu erweitern und zu optimieren. Design Science Research ist in erster Linie Forschung unter Verwendung von Design als Forschungsmethode oder -technik und wird definiert als Lernen durch das Erzeugen von Artefakten (u.a. Vaishnavi et al., 2019). Folgende Artefakte werden im Rahmen von Prim-E-Proof entwickelt (siehe Abb. 1):

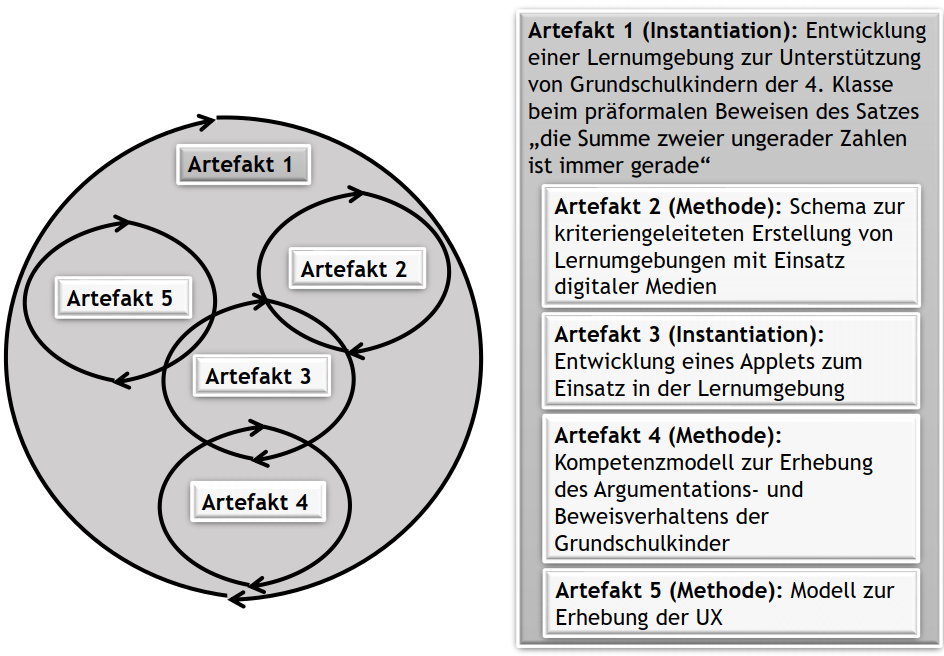
Abb. 1: Artefakte, die im Rahmen von Prim-E-Proof entwickelt werden

Design Science Research wird im vorliegenden Projekt auf den Bildungskontext zur Entwicklung einer Lernumgebung (Artefakt 1) übertragen, indem das Four Cycle Modell (Drechsler & Hevner, 2016) mit dem Dortmunder Modell (Hußmann et al., 2013; Prediger et al., 2012) kombiniert wird. Das Dortmunder Modell wird in eine Cycle View implementiert und durch den Change and Impact Cycle erweitert (siehe Abb. 2, um so eine Entwicklung von Lernumgebungen im Rahmen „guter“ Design Science Research zu unterstützen, die nach Hevner (2007) nicht nur durch praktische Nutzbarkeit eines Artefakts ausgezeichnet ist, sondern auch durch die Synergie zwischen Relevanz und Sorgfalt und den Beitrag entlang Relevance Cycle und Rigor Cycle.

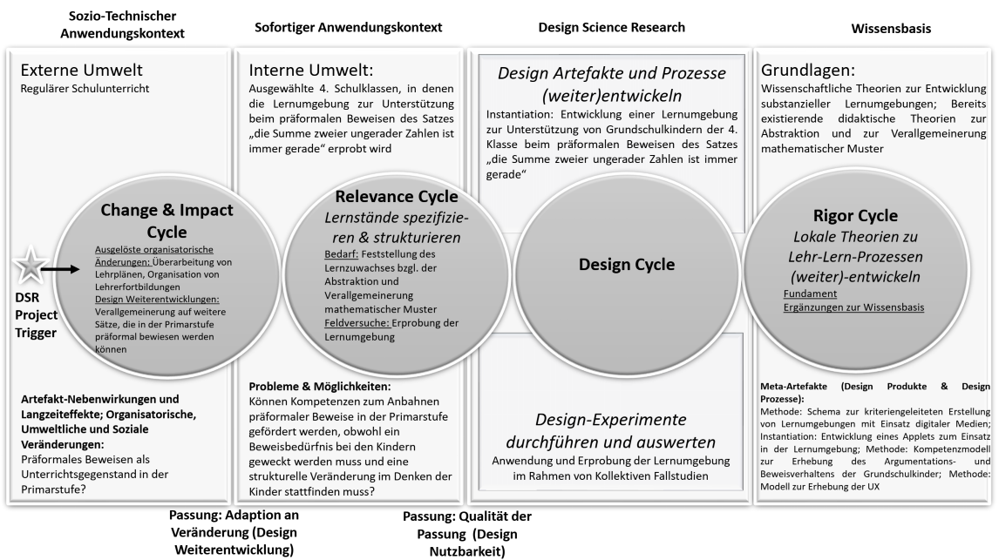
Abb. 2: Kombination des Four-Cycle-Modells (Drechsler & Hevner, 2016) und des Dortmunder Modells (u.a. Prediger et al., 2012) und Anwendung auf die Lernumgebung

Zur Entwicklung der substanziellen Lernumgebungen werden u.a. Leitideen nach Wollring (2008) und Kriterien nach Wittmann (1995) beachtet. Ein Entscheidungsunterstützungssystem zur Auswahl passender Apps für den Mathematikunterricht der Grundschule (Platz, 2019c) kann unterstützend bei der didaktischen Reflexion von digitalen Medien eingesetzt in Lernumgebungen wirken, da sich das Potenzial digitaler Medien nur dann entfalten kann, wenn diese inhaltlich sinnvoll und didaktisch reflektiert eingesetzt werden (Platz, 2019c). Um die Wirksamkeit der entwickelten Lernumgebungen zu untersuchen, werden Collective Case Studies (u.a. Stake, 2008) mit der Fragestellung, welche epistemischen Aktionen in den Argumentations- und Beweistätigkeiten der Schüler*innen erkennbar werden, durchgeführt. Abstraction in Context (Dreyfus & Kidron, 2014) wird dabei zur Datenanalyse angewendet. Abstraction in Context stellt Werkzeuge bereit, mit denen Rückschlüsse auf die Denkprozesse der Lernenden gezogen werden können und versucht eine Brücke zwischen kognitiven und lokalisierten Abstraktionstheorien sowie zwischen konstruktivistischen und aktivitätsorientierten Ansätzen zu schlagen (Dreyfus & Kidron, 2014). Zur Darstellung des Argumentationsprozesses wird ein Schema verwendet, welches u.a. an Toulmin (1958) orientiert ist. Um den gesamten Prozess der Argumentation und der Beweisentwicklung erfassen zu können, wurde dieses durch die Darstellung der Widerlegung von Argumenten sowie die Struktur des Argumentationsprozesses erweitert (Platz, 2019a; Platz & Schlicht, im Druck).

Durch die generische Konzeption des Prototypen sowie das Zurverfügungstellen als OpenSource und OpenContent, kann dieser sowohl international als auch in verschiedenen Bildungskontexten (z.B. im Schulkontext, im Lehramts- oder Ingenieurstudium, etc.) eingesetzt werden.
In der Lehramtsausbildung könnte dieses Projekt u.a. durch die eigenständige Konzeption von Lernumgebungen mit digitalen Medien zur Unterstützung von Argumentations- und Beweisfähigkeiten (u.a. in der Primarstufe) im Rahmen von Seminaren wie bspw. Fachdidaktischen Ergänzungen oder Vertiefungen aufgegriffen werden. Diese Lernumgebungen könnten bspw. in Kooperation mit Studierenden der Informatik programmiertechnisch als OpenSource Applets auf Tablet PCs umgesetzt und unterrichtspraktisch getestet und evaluiert werden.
Die Umsetzung muss nicht auf OpenSource Applets auf Tablet PCs beschränkt bleiben: Es könnten Lernumgebungen, die geometrische Beweise behandeln, beispielweise mittels (digitalen) additiven Fertigungstechnologien (3D-Druck) umgesetzt werden.

Der 3D-Druck kann dabei ein besonderes Potenzial bezüglich Beweisen zur räumlichen Geometrie ausschöpfen.
Ferner könnten Arbeitsmittel mit Hilfe des 3D-Drucks durch die Studierenden für ihre Lernumgebungen erstellt werden. Auch der Einsatz von CAD-Software durch Schüler*innen könnte in die Lernumgebungen implementiert werden, um so in der CAD-Software erstellte (zweidimensional dargestellte) Elemente im dreidimensionalen Raum auszudrucken.

Angelehnt ist dieses Konzept an das „Lernen durch Lehren“, da die Studierenden sich durch die Entwicklung von Lernumgebungen zu bestimmten Beweisen selbst sowohl fachlich als auch didaktisch mit dem jeweiligen Beweis auseinandersetzen müssen und ein tiefgreifendes Beweisverständnis entwickeln müssen, um eine Lernumgebung erstellen zu können.

Sogar auf den Einsatz in Entwicklungsländern könnten solche Lernumgebungen, die im Rahmen von Prim-E-Proof erstellt werden, übertragen werden. Dies ist sehr wichtig, da in solchen Ländern von vielen Einwohnern die Grundschule meist die einzige Schulform ist, die besucht wird und Argumentationskompetenzen sowie logisches Schlussfolgern in vielen fächerübergreifenden Kontexten für ein erfolgreiches Leben – in Entwicklungsländern in Risikosituationen im gravierendsten Fall sogar für das Überleben – essentiell sind.

Literatur

• Blum, W., & Kirsch, A. (1991). Preformal proving: Examples and reflections. Educational Studies in Mathematics, 22(2). New York: Springer Publishing Company, 183–203.
• Drechsler, A., & Hevner, A. (2016). A four-cycle model of IS design science research: capturing the dynamic nature of IS artifact design. In Breakthroughs and Emerging Insights from Ongoing Design Science Projects: Research-in-progress papers and poster presentations from the 11th International Conference on Design Science Research in Information Systems and Technology (DESRIST) 2016. St. John, Canada, 23-25 May. DESRIST 2016.
• Dreyfus, T., & Kidron, I. (2014). Introduction to abstraction in context (AiC). In A. Bikner-Ahsbahs, & S. Prediger (Eds.), Networking of theories as a research practice in mathematics education (pp. 85–96). Cham: Springer.
• Fischer, H., & Malle, G. (2004). Mensch und Mathematik. Eine Einführung in didaktisches Denken und Handeln. Wien: Profil.
• Götze, D. (2019). Arithmetisches Verständnis bei Grundschulstudierenden fördern – Konzeptionelles und Beispiele aus dem Projekt „Arithmetik digital“. In R. Rink, & D. Walter (Hrsg.), Beiträge zum 5. Band der Reihe „Lernen, Lehren und Forschen mit digitalen Medien“. Digitale Medien in der Lehreraus- und -fortbildung von Mathematiklehrkräften – Konzeptionelles und Beispiele (S. 115–132). Münster: WTM-Verlag.
• Grieser, D. (2015). Mathematisches Problemlösen und Beweisen: Entdeckendes Lernen in der Studieneingangsphase. In J. Roth, T. Bauer, H. Koch, & S. Prediger (Hrsg.), Übergänge konstruktiv gestalten (S. 87–102). Wiesbaden: Springer.
• Hevner, A. R. (2007). A three cycle view of design science research. Scandinavian journal of information systems, 19(2), 4, 1–6.
• Hußmann, S., Thiele, J., Hinz, R., Prediger, S., & Ralle, B. (2013). Gegenstandsorientierte Unterrichtsdesigns entwickeln und erforschen – Fachdidaktische Entwicklungsforschung im Dortmunder Modell. In M. Komorek, & S. Prediger (Hrsg.), Der lange Weg zum Unterrichtsdesign: Zur Begründung und Umsetzung genuin fachdidaktischer Forschungs- und Entwicklungsprogramme (S. 25–42). Münster: Waxmann.
• Huth, M. (2013).Mathematische Gestik und Lautsprache von Lernenden. In G. Greefrath, F. Käpnick, & M. Stein (Hrsg.), Beiträge zum Mathematikunterricht 2013 (S. 492–495). Münster: WTM-Verlag.
• Kothe, S. (1979). Gibt es Entwicklungsmöglichkeiten für ein Beweisbedürfnis in den ersten Schuljahren? In W. Dörfler, & R. Fischer (Hrsg.), Beweisen im Mathematikunterricht: Vorträge des 2. Internationalen Symposiums für „Didaktik der Mathematik“ von 26.9. bis 29.9. 1978 in Klagenfurt (S. 275–282). Wien: Verlag Hölder-Pichler-Tempsky.
• Krauthausen, G. (2018). Einführung in die Mathematikdidaktik – Grundschule. Berlin: Springer.
• Lambert, A. (2012). Was soll das bedeuten?: Enaktiv-ikonisch-symbolisch. Aneignungsformen beim Geometrielernen. In A. Filler, & M. Ludwig (Hrsg.), Vernetzungen und Anwendungen im Geometrieunterricht. Ziele und Visionen 2020 (S. 5–32). Hildesheim: Franzbecker.
• Platz, M. (2019a). Learning environments applying digital learning tools to support argumentation skills in primary school: first insights into the project. In U. T. Jankvist, M. van den Heuvel-Panhuizen, & M. Veldhuis (Eds.), Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (CERME11, 6.-10.2.2019) (pp. 2908–2915). Utrecht, Netherlands: Freudenthal Group, in collaboration with the Freudenthal Institute, Utrecht University & ERME.
• Platz, M. (2019b). Das Wendeplättchen-Applet – Potenziale und Grenzen eines Einsatzes in Lernumgebungen für den Primarstufenbereich. In G. Pinkernell, & F. Schacht (Hrsg.), Digitales Lernen im Mathematikunterricht. Arbeitskreis Mathematikunterricht und digitale Werkzeuge in der Gesellschaft für Didaktik der Mathematik (S. 121–132). Hildesheim: Franzbecker.
• Platz, M. (2019c). Vorstellung eines Entscheidungsunterstützungssystems zur Auswahl passender Apps und Applets für den Mathematikunterricht der Grundschule. In R. Rink, & D. Walter (Hrsg.), Beiträge zum 5. Band der Reihe „Lernen, Lehren und Forschen mit digitalen Medien“. Digitale Medien in der Lehreraus- und -fortbildung von Mathematiklehrkräften – Konzeptionelles und Beispiele (S. 167–182). Münster: WTM-Verlag.
• Platz, M. (im Druck). Lernumgebungen mit digitalen Medien zur Unterstützung von Argumentations- und
  Beweiskompetenzen in der Primarstufe – Der aktuelle Stand des Projektes „Prim-E-Proof“. In B. Brandt, L. Bröll, & H. Dausend (Hrsg.), Digitales Lernen in der Grundschule II. Aktuelle Trends in Forschung und Praxis. Münster: Waxmann Verlag.
• Platz, M. (angenommen). Abstraction in Context zur Optimierung einer Lernumgebung zum präformalen Beweisen mit digitalen Medien in der Primarstufe. In Beiträge zum 6. Band der Reihe „Lernen, Lehren und Forschen mit digitalen Medien.“ Münster: WTM-Verlag.
• Platz, M., Krieger, M., Niehaus, E., & Winter, K. (2018). Suggestion of an E-proof Environment in Mathematics Education. In D. R. Thompson, M. Burton, A. Cusi, & D. Wright (Eds.), ICME 13 Monographs – Classroom Assessment in Mathematics: Perspectives from around the Globe (pp. 107–120). Cham: Springer.
• Platz, M. & Schlicht, S. (im Druck). Enhancing Childrens‘ Argumentation Skills in Primary Schools using Digital Learning Tools – Interpretative Analysis of a first draft Learning Environment. In ICTMT14 Conference Proceedings. 14th International Conference on Technology in Mathematics Teaching, 22.-25.07.2019 in Essen. DuEPublico Repostitory, Universitätsbibliothek Duisburg-Essen.
• Plomp, T. (2013). Educational design research: An introduction. In T. Plomp & N. Nieveen (Hrsg.), Educational
  Design Research (pp. 11–50). Netzodruk, Enschede: SLO – Netherlands institute for curriculum development.
• Prediger, S., Link, M., Hinz, R., Hußmann, S., Thiele, J., & Ralle, B. (2012). Lehr-Lernprozesse initiieren und erforschen – Fachdidaktische Entwicklungsforschung im Dortmunder Modell. MNU 65(8), 452–457.
• Stake (2008) Case Studies. In Denzin, N. K., & Lincoln, Y. S. (Eds.). Strategies of qualitative inquiry (Vol. 2) (pp. 134 — 164. Thousand Oaks: Sage.
• Stylianides, A. J. (2016). Proving in the elementary mathematics classroom. Oxford: Oxford University Press.
• Toulmin, S. E. (1958). The Uses of Argument. Cambridge: Cambridge University Press (2003).
• Vaishnavi, V., Kuechler, W., & Petter, S. (2019). Design Science Research in Information Systems. January 20, 2004 (created in 2004 and updated until 2019 by Vaishnavi, V. and Kuechler, W.). Verfügbar unter http://www.desrist.org/design-research-in-information-systems/.
• Walter, D. (2017). Nutzungsweisen bei der Verwendung von Tablet-Apps. Cham: Springer.
• Wittmann, E. (1995). Unterrichtsdesign und empirische Forschung. In K. P. Müller (Hrsg.), Beiträge zum Mathematikunterricht (S. 528–531). Hildesheim.
• Wittmann, E. (2014). Operative Beweise in der Schul- und Elementarmathematik. mathematica didactica, 37, 213–232.
• Wollring, B. (2008). Zur Kennzeichnung von Lernumgebungen für den Mathematikunterricht in der Grundschule. In Kasseler Forschergruppe (Hrsg.), Lernumgebungen auf dem Prüfstand. Bericht 2 der Kasseler Forschergruppe Empirische Bildungsforschung Lehren – Lernen – Literacy (S. 9–26). Kassel: kassel university press GmbH.